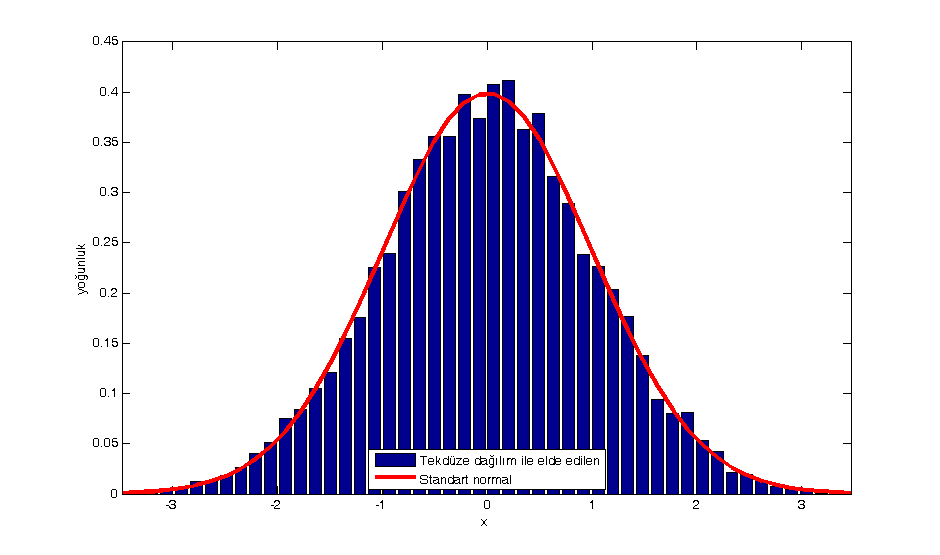
Tekdüze dağılımdan standart normale
Elimizde yalnızca tekdüze (birörnek, uniform) dağılıma ait rand fonksiyonu olsun. Bu fonksiyonu kullanarak standart normal dağılımdan gelen rassal değişkenler elde etmek istiyoruz.
Yani, alttaki tekdüze dağılım ile
\begin{align}
u \sim \mathcal{U}(u;0,1)
\end{align}
aşağıda verildiği gibi bir standart normal dağılım üretmek istiyoruz:
\begin{align}
z \sim \mathcal{N}(z;0,1)
\end{align}
Merkezi limit teoremini hatırlayalım ve şimdilik tekdüze durumunu ele alalım: Standart tekdüze dağılımdan gelen $n$ adet örneğin toplamları, normal dağılıma benzer şekilde dağılır. Bu özdeş ve birbirinden bağımsız değişkenlerin toplamının beklenen değeri $n/2$, varyansı ise $n/12$ olur. Çünkü herbir $u_i$’nin beklenen değeri $1/2$, varyansı ise $1/12$.
Öyleyse bir örneklemin toplamından $n/2$ çıkarıp, standart sapma olan $\sqrt{n/12}$’ye bölersek yeni değer standart normal dağılımdan gelmiş olur. Tabi bu yaklaşımın başarılı olabilmesi için $n$’nin değerinin büyük olması önemli. Tekdüze dağılımda $n=12$ alsak dahi fena sonuç vermiyor:
m = 10000; % Deney sayısı
n = 12; % Her deneyde ortalaması alınan rastsal değişken sayısı
% x'ler tek tek rastsal değişkenler olsun, y ise onların ortalaması olan rassal değişken
y = zeros(1,m);
for i = 1:m
u = rand(1,n); % Tekdüze dağılım
y(i) = sum(u);
end
z = (y-n/2)/sqrt(n/12);
% 10000 tane rastsal değişkenin histogramını bulalım
[f,u] = hist(z,50);
% Düzgelenmiş histogramı çizelim
bar(u,f/trapz(u,f));hold on
% Histogram üstüne standart normal dağılım grafiğini çizelim
plot(u,normpdf(u,0,1),'r', 'Linewidth', 3);hold off
axis([min(u) max(u) 0 0.45])
xlabel('x')
ylabel('yoğunluk')
h = legend('Tekdüze dağılım ile elde edilen', 'Standart normal', ...
'Location', 'South');