Mahalanobis uzaklığı
Uzayda iki nokta arasındaki mesafeyi ölçmek için kullandığımız en temel uzaklık ölçütü şu hepimizin bildiği Öklid uzaklığıdır. Matematiksel olarak ifade edersek herhangi $\mathbf{x}$ ve $\mathbf{y}$ noktaları (vektörleri) arasındaki Öklid uzaklığı
$$d = \|\mathbf{x}-\mathbf{y}\|_2 = \sqrt{(\mathbf{x}-\mathbf{y})’ (\mathbf{x}-\mathbf{y})}$$
biçiminde hesaplanır. Bu uzaklık, bahsi geçen iki nokta dışındaki bilgileri hesaba katmaz. Ve bu noktaların tanımlı olduğu eksenlerin birimlerini eşit kabul eder. Fakat gerçek hayatta işler pek böyle işlemez. Eksenlerin birimleri genelde birbirinden farklı değerlerde ve değişintidedirler; armutlarla elmalar toplanmaz. Örneğin bir eksen boyunca değerler -100 ile 100 arasında seyrederken, diğer eksendeki değerler 0.1 ile 0.2 arasında farklılık gösteriyor olabilir. Hal böyle iken bir eksendeki 5 birimlik farkı ciddiye almazken, diğer eksende çok aykırı bir konuma uçmuş olabiliriz.
Komşuluğa bağlı sınıflandırma yapmak (ör: en yakın komşu), noktaları öbeklemek veya aykırı noktaları bulmak için geliştirdiğimiz algoritmalarda kullanmak hevesiyle daha uygun bir uzaklık ölçütü isteriz. İşte, Mahalanobis uzaklığı bu durumlarda kullanılabilecek uygun bir uzaklık ölçütüdür. Mahalanobis uzaklığı iki noktanın arasındaki mesafeyi hesaplamak için veriden hesaplanan kovaryans (özdeğişinti) matrisini hesaba katar. Dolayısıyla diğer noktaların davranışını da hesaba katmış olur. Matematiksel olarak ifade edecek olursak $\mathbf{C}$ veriden elde edilen kovaryans matrisini ifade etmek üzere, herhangi $\mathbf{x}$ ve $\mathbf{y}$ noktaları (vektörleri) arasındaki Mahalanobis uzaklığı
$$d = \sqrt{(\mathbf{x}-\mathbf{y})’ \mathbf{C}^{-1} (\mathbf{x}-\mathbf{y})}$$
biçiminde hesaplanır. Aradaki kovaryans matrisinin tersi ile çarpma işlemi, elde edilen uzaklığın o doğrultuda hesaplanan değişinti (varyans, standart sapmanın karesi) ile bölünmesi gibi yorumlanabilir. Yani elde edilen uzaklığın birimi, iki nokta arasından geçen doğrunun doğrultusu boyunca olan standart sapma cinsindendir. Bu da elbette veriye bağlı bir değerdir.
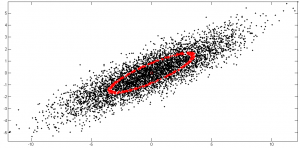
Örnek 2B veri üstünde, merkeze (yaklaşık) 1 birim uzaklıktaki noktaları gözlemlemek için alttaki MATLAB kodunu yazdım. Bu kodla oynayarak (örneğin kodun başlangıcındaki dönüşüm matrisini değiştirerek) farklı durumlar için uzaklığın nasıl olacağını kendiniz test edebilirsiniz. Siyahlar tüm örnek noktaları, kırmızılar ise referans noktaya (şekildeki referans merkez) yaklaşık 1 birim uzaklıktaki noktaları ifade ediyor.
Not: Koddaki döngüyü vektörize hale getirmek mümkün fakat anlaşılabilirlik açısından gözüme bu daha uygun göründü.
clc,clear
A = [0.7 -0.3; 0.3 0.7] * [5 0; 0 1]; % Ölçekleme ve döndürme
% A = [4 -0.2;2 0.7]; % Başka bir dönüşüm
xRef= [0 0]'; % Uzaklık için referans nokta. Merkez için [0 0]' yapın
N = 5000; % Nokta sayısı
X = A*randn(2,N);
% A ile dönüştürülmüş (yaklaşık) birim çember içindeki rastgele noktalar
C = cov(X'); % Kovaryans (değişinti) matrisi
pinvC = pinv(C); % ve tersi (döngüde tekrar tekrar hesaplamamak için)
d = zeros(1,N); % Uzaklıklar
for i = 1:N
d(i) = sqrt((X(:,i)-xRef)' * pinvC * (X(:,i)-xRef));
end
idx = abs(d-1.0) < 0.05;
% Referans ile uzaklığı yaklaşık 1.0 olan noktaların indisleri
% Buradaki 1.0 birimi, iki noktanın doğrultusundaki standart sapma
% cinsindendir.
% Tüm noktaları siyah çiz, 1.0 uzaklığındakileri kırmızı çiz
plot(X(1,:), X(2,:), 'k.')
hold on
plot(X(1,idx), X(2,idx), 'r*')
plot(xRef(1), xRef(2), 'ro')
hold off
axis equal tight

