MATLAB Programlamaya Giriş
Not: Bu kaynaktan dilediğiniz şekilde yararlanabilirsiniz. MATLAB ile ilgili eğitim videoları için Açık Ders projesine göz atabilirsiniz.
Görüntü işleme kodlarını anlamak için öncelikle MATLAB bilmek gerekiyor. Biraz baktım da, internette derli toplu Türkçe bir MATLAB programlama kaynağı yok. Daha doğrusu olanlar o kadar yavaş ilerliyor ki… Programlama bilip de hızlıca MATLAB öğrenmek isteyenlere pek uygun gözükmüyor. Güzel bir kaynak olduğunu düşündüğüm kodları açıklamalarıyla birlikte göndereyim istedim.
Aşağıdaki kodları MATLAB komut satırına sırası ile girip sonuçlarını gözlemleyerek güzel bir başlangıç yapabilirsiniz.
Şimdilik yüzeysel bir ders (‘tutorial’) oldu.. Biraz (!) zamanımı alıyor açıkçası. Eklemeler olursa sonraki yazı(lar)da genişletirim.
Buyurun, temel MATLAB programlamaya hızlıca giriş notları…
Başlamadan
% sembolü yorumlar icin kullanılır (satır sonuna kadar). İpucu: Birden fazla satır icin hataAyiklama diye global bir değişken tanımlayıp
if hataAyiklama islemler end
şeklinde yazabilirsiniz.
Tek satırda kullanmak için oldukça uzun olan bir işlem yazacağınız zaman alt satıra geçtiğinizi belirtmek amacıyla satır sonuna ... ekleyin. Ör:
A = [1, 2; ...
3, 4];
İşlem sonuna noktalı virgül konulursa MATLAB sonucu ekrana basmaz. Eğer ; eklemezseniz sonuç görüntülenir. Değişkenlerin değerlerini görmek için faydalıdır. Ör:
A
İşlere girişmeden önce clear ile ortamdaki değişkenleri temizleyelim ve clc ile de komut ekranını temizleyelim
clear clc
MATLAB komut satırı komut sistemine (kabuk) benzetilebilir:
- Komutları tekrar yazmak yerine yukarı oku kullanın ( benzer şekilde geçmişte ileriye gitmek için ise aşağı oku kullanabilirsiniz) Önce birkaç karakter yazarsanız, yukarı/aşağı okla o karakterlerle başlayan komutları gezebilirsiniz. Bu size çok hız kazandıracaktır.
Komut satırındayken “tab” komut tamamlamaya yarar.
Basit hata ayıklama: Eğer dbstop if error çalışma sırasında hata veren bir betiği/fonksiyonu çalıştırmadan önce yazılmışsa, program hatanın olduğu yerde durur. Hata ayıklamak için çok işe yarayabilir. Ama bana kalırsa en temizi “breakpoint” koyarak hata ayıklamaktır. Program o noktaya geldiğinde istediğiniz değişkeni gözlemleyebilirsiniz. Ayrıntılı kullanım için şu ve şu videoyu izlemenizi tavsiye ederim.
MATLAB’de Temel Veri Yapıları
MATLAB’de temel yapılar:
Skalar sayılar ( genellikle “double”-kesinliğinde gerçel sayılar), vektörler ve matrislerdir:
Not: Aslında bunların hepsi birer matristir. Örneğin skalar bir sayı 1×1’lik bir matrisdir.
2×2’lik matrisler yaratalım. Matris yaratmanın en basit yolu elemanlarını kare parantez içinde yazmaktır. ; sembolu satırları, (isteğe bağlı) , ise sütunlari ayırır.
A = [1 2; 3 4]; B = [1,2; 3,4];
Görüldüğü üzere noktalı virgülle bitirdiğimiz için sonuçlar ekrana basılmadı. Şimdi skalar bir değer oluşturalım.
Ben örneklerde, sonuçları görmek için sonlarına ; eklemeyeceğim. Siz isterseniz ekleyebilirsiniz. Sonuçları bize döndürdüğü için MATLAB’i çok gelişmiş bir hesap makinesi olarak düşünebiliriz.
N = 5
N = 5
Satır ve sütun vektörleri oluşturalım. Matris tanımı içinde ; kullanırsak alt satıra geç demek oluyor.
v = [1 0 0] v = [1; 2; 3]
v = 1 0 0 v = 1 2 3
v vektörünün transpozesini alalım.
Dikkat: Tek tırnak sembolü eşlenik transpoze (conjugate tronspose) içindir. Karmaşık sayılarla çalışırken hangisini kullandığınız önemlidir.
v = v.'
v = 1 2 3
Vektör değerlerini teker teker yazmak zor sanki böyle. Gelin kolayına kaçıp belli aralıklar ile doldurulmus vektör oluşturalım.
Kullanım: [baslangic:adım:bitis]
v = 1:.5:3 v = pi*[-4:2:4]/4
v = 1.0000 1.5000 2.0000 2.5000 3.0000 v = -3.1416 -1.5708 0 1.5708 3.1416
Başka bir yol da mümkün: linspace(baslangic,bitis,kac_parca)
v = linspace(1,3,5)
v = 1.0000 1.5000 2.0000 2.5000 3.0000
Peki boş değişken oluşturmak isteseydik
v = []
v = []
Özel matrisler oluşturma:
İlk parametre satır sayısını, 2. parametre sütun sayısını belirtir.
2×3’lük sıfır ve bir matrisleri oluşturalım:
m = zeros(2, 3) v = ones(2, 3)
m = 0 0 0 0 0 0 v = 1 1 1 1 1 1
3×3’lük birim matris oluşturalım:
m = eye(3)
m = 1 0 0 0 1 0 0 0 1
Rastgele sayılar içeren 3×1’lik bir matris (sütun vektörü) oluşturalım.
rand‘ın yardım tanımına bakınız.v = rand(3, 1)
v = 0.9436 0.4269 0.0331
Dikkat: Eğer iki değil de bir parametre verirsek, örnekteki 3×3’lük matris gibi sıfır matrisi oluşturur (vektör değil!)
m = zeros(3)
m = 0 0 0 0 0 0 0 0 0
Vektör ve matrisleri indisleme:
Uyarı: İndisler her zaman 1 ile başlar (0 ile değil)!
Vektör elemanına ulaşma
v = [1 2 3]; v(3)
ans = 3
2. elemanı silmek isteseydik
v(2) = []
v = 1 3
Matrisin bir elemanına ulaşmak için matris(satırNo, sutunNo)
m = [1 2 3 4; 5 7 8 8; 9 10 11 12; 13 14 15 16] m(1, 3)
m = 1 2 3 4 5 7 8 8 9 10 11 12 13 14 15 16 ans = 3
Matrisin bir satırının tümüne ulaşma (2. satır) ve bir sütununun tümüne ulaşma (1. sütun)
m(2, :) m(:, 1)
ans = 5 7 8 8 ans = 1 5 9 13
1. satırın 1’den 3’e kadar (dahil) elemanları
m(1, 1:3)
ans = 1 2 3
2. sütunun 2’den 3’e kadar (dahil) elemanları
m(2:3, 2)
ans = 7 10
Anahtar sözcük end satır/sütun’daki son elemana kadar demektir:
m(2:end, 3)
ans = 8 11 15
Matrisin boyutunu gösterelim
m = [1 2 3; 4 5 6] size(m)
m = 1 2 3 4 5 6 ans = 2 3
Satır sayısı:
size(m, 1)
ans = 2
Sütun sayısı:
size(m, 2)
ans = 3
m ile aynı boyutta yeni bir matris oluşturmak istersek:
m1 = zeros(size(m))
m1 = 0 0 0 0 0 0
Şu ana kadar bir hayli çalıştık. Çalışma alanındaki değişkenleri görelim:
who
Your variables are: A B N ans m m1 v
Değişkenleri boyut, tip, vb. bilgileriyle görelim:
whos
Name SizeBytes Class Attributes A 2x2 32 double B 2x2 32 double N 1x1 8 double ans 1x1 8 double m 2x3 48 double m1 2x3 48 double v 1x2 16 double
Bu arada, ans diye gözüken değişken en son yaptığımız ve herhangi bir değişkene atamadığımız değer. Yani answer demek.
Vektör ve Matrisler Üzerinde Basit İşlemler
Eleman bazında yapılan işlemler:
Bu işlemler “eleman eleman” yapılan işlemlerdir. Eğer iki vektör/matris toplama, çıkarma, çarpma veya bölme işlemine sokulacaksa aynı boyutta olmalıdır.
Sütun vektörünü skalar ile çarpma ve skalara bölme:
a = [1 2 3 4]'; 2 * a
ans = 2 4 6 8
a / 4
ans = 0.2500 0.5000 0.7500 1.0000
Vektörlerde toplama (matrislerde de aynı) ve çıkarma:
b = [5 6 7 8]'; a + b
ans = 6 8 10 12
a - b
ans = -4 -4 -4 -4
Eleman eleman kare alma, çarpma ve bölme. .‘ya dikkat edin! Normal semboller matris çarpma ve bölmesi demek!
a .^ 2
ans = 1 4 9 16
a .* b
ans = 5 12 21 32
a ./ b
ans = 0.2000 0.3333 0.4286 0.5000
Eleman eleman logaritma alma ve en yakın tamsayıya yuvarlama:
log([1 2 3 4])
ans = 0 0.6931 1.0986 1.3863
round([1.5 2; 2.2 3.1])
ans = 2 2 2 3
Benzer sekilde eleman eleman işlem yapabilen birçok fonksiyon vardır. Örneğin floor ve ceil
ipucu: MATLAB yorumlayıcı olduğu için döngülerde yavaş çalışır. O yüzden kullanacağınız işlemleri eleman bazında işlemler şeklinde tanımlamak işleri hızlandırır. Bakınız: (4) Vektörleme.
Vektör işlemleri
Vektörlerde işlem yapan önceden tanımlı bazı MATLAB fonksiyonlarına bakalım.
a = [1 4 6 3]
a = 1 4 6 3
Vektör elemanlarının toplamı:
sum(a)
ans = 14
Vektör elemanlarının aritmetik ortalaması:
mean(a)
ans = 3.5000
Vektör elemanlarının değişintisi (varyans):
var(a)
ans = 4.3333
Standart sapma:
std(a)
ans = 2.0817
En yüksek ve en düşük değerler:
max(a)
ans = 6
min(a)
ans = 1
Eğer matris üzerinde işlem yapılırsa, bu fonksiyonlar matrisin her bir sütununda işlem yaparlar ve sonuç olarak bir satır vektörü döndürürler
a = [1 2 3; 4 5 6]
a = 1 2 3 4 5 6
Her sütunun ortalaması:
mean(a)
ans = 2.5000 3.5000 4.5000
Her sütunun en yüksek değeri:
max(a)
ans = 4 5 6
Matristeki en yüksek değer:
max(max(a))
ans = 6
veya
max(a(:))
ans = 6
Her satırın ortalaması (ikinci argüman hangi boyutta işlem yapılacagını gösterir):
mean(a, 2)
ans = 2 5
Vektörlerde çarpma ve bölme işlemlerine geçelim. 1×3’lük satır vektörü ile 3×1’lik sütun vektörü çarpımı sonucu skalar elde ederiz. İç çarpım olarak da bilinir. . kullanmadığımıza dikkat edin.
[1 2 3] * [4 5 6]'
ans = 32
3×1 sütun vektörü ile 1×3’lük satır vektörü çarpımı 3×3’lük matris oluşturur.
[1 2 3]' * [4 5 6]
ans = 4 5 6 8 10 12 12 15 18
Matris işlemleri:
İki tane rasgele matris oluşturup çarpalım. Alttaki örnekte çarpım sonucu 3×4’lük bir matris olacak:
a = rand(3,2) b = rand(2,4) c = a * b
a = 0.9294 0.2600 0.9250 0.7869 0.3583 0.5116 b = 0.5625 0.0924 0.9429 0.8459 0.6848 0.8726 0.0966 0.9094 c = 0.7009 0.3127 0.9015 1.0226 1.0592 0.7721 0.9482 1.4980 0.5519 0.4795 0.3873 0.7683
Vektör ve matrislerle başka denemeler yapalım:
a = [1 2; 3 4; 5 6]; b = [5 6 7]; b * a
ans = 58 76
c = [8; 9]; a * c
ans = 26 60 94
Matrisin tersini hesaplayalım:
a = [1 3 2; 6 5 4; 7 8 9]; inv(a)
ans = -0.3333 0.2821 -0.0513 0.6667 0.1282 -0.2051 -0.3333 -0.3333 0.3333
a‘nın özdeğerlerinden oluşan vektör:
eig(a)
ans = 15.1601 -1.6860 1.5258
Hesaplamışken özvektörleri de bulalım. D matrisi köşegende özvektörleri barındırır; V matrisi özvektörleri içerir. Bu, MATLAB ile birden çok değişken döndürülmesine de güzel bir ornek!
F1‘e basarak MATLAB Yardım belgelerini açabilir ve arama yapabilirsiniz.[V, D] = eig(a)
V = -0.2199 -0.7374 -0.2033 -0.4671 0.6751 -0.5675 -0.8564 -0.0224 0.7979 D = 15.1601 0 0 0 -1.6860 0 0 0 1.5258
a‘nın tekil değer ayrışımı sonucu. a = U * S * V', a‘nın “singular” değerleri S‘de bulunur
[U, S, V] = svd(a)
U = -0.2097 0.4071 -0.8890 -0.5147 -0.8190 -0.2536 -0.8313 0.4044 0.3813 S = 16.7157 0 0 0 2.0802 0 0 0 1.1216 V = -0.5454 -0.8059 0.2302 -0.5895 0.1736 -0.7889 -0.5959 0.5660 0.5697
Başka başka da matris fonksiyonları var: det, norm, rank, …
Matrisleri yeniden şekillendirme ve birleştirme:
Önce bir matris oluşturalım. Daha sonra onu doğrusal bir vektöre çevirelim.
Dikkat: Matrisleri diğer dillerdeki (c, c++, vb.) gibi satır satır değil de sütun sütun düşünmek gerekir. a‘nın sütunlarını ekleyerek yeni bir sütun vektörü oluşturuyoruz:
a = [1 2; 3 4; 5 6]; b = a(:)
b = 1 3 5 2 4 6
Tüm elemanların toplamını almak isteseydik:
sum(a(:))
ans = 21
b vektörünün elemanlarından 2×3’lük bir matris oluşturalım (yine sütun sütun):
a = reshape(b, 2, 3)
a = 1 5 4 3 2 6
horzcat‘a bakınız.İki tane satır vektörünü yatay olarak birleştirelim.
a = [1 2]; b = [3 4]; c = [a b]
c = 1 2 3 4
vertcat‘a bakınız.İki tane sütun vektörünü dikey olarak birleştirelim.
a = [1; 2; 3]; b = [4; 5] c = [a; b]
b = 4 5 c = 1 2 3 4 5
Benzer şekilde matrisleri de birleştirebiliriz:
a = [eye(3) rand(3)]
a = 1.0000 0 0 0.0113 0.3851 0.5757 0 1.0000 0 0.5237 0.6493 0.6319 0 0 1.0000 0.6503 0.7629 0.2782
b = [eye(3); ones(1, 3)]
b = 1 0 0 0 1 0 0 0 1 1 1 1
repmat kullanarak bir değişkeni ızgara şeklinde kopyalayabiliriz. Örneğin tüm değerleri 5 olan 3×2’lik bir matris yapalım.
b = repmat(5, 3, 2)
b = 5 5 5 5 5 5
İlla ki tek değer olması gerekmezdi. Bir matrisi de klonlayabilirdik.
Kullanım: repmat(kopyalanacak_veri, satir_sayisi, sutun_sayisi)
b = repmat([1 2; 3 4], 1, 2)
b = 1 2 1 2 3 4 3 4
Verilen vektörle 3×3’lük bir köşegen matrisi oluşturalım:
b = diag([1 2 3])
b = 1 0 0 0 2 0 0 0 3
Kontrol İşlemleri ve Vektörleme (Vectorization)
Döngüleri en azından bir dilde bildiğinizi bilerek hızlıca MATLAB’de nasıl olduğuna bakalım.
Kontrol işlemlerinin sözdizimi:
for değişken = değerler işlem ... işlem end
deferler döngünün hangi değerler icin yapılacağı vektör olmalıdır, örneğin: 1:10 veya -1:0.5:1 veya [1 4 7]
while kosul islemler end
if kosul islemler elseif kosul islemler else islemler end
elseif ve else kısımları isteğe bağlıdır, end ise gereklidir.
kosullar genellikle ilişkilerden oluşur, örneğin a < b.
Operatörler: ~, <, >, <=, >=, ==, ~= (C'deki ! yerine ~ kullanılır.) kosullar, && (ve) || (veya) ile kullanılabilir. Ör. a < b && ( c != d || e >= f)
Uyarı: Döngüler MATLAB'de çok yavaş çalışır. İşlemlerinizi hızlandırmak için mümkün olan yerlerde vektörleme yapmalısınız. Ör: Kodunuzu matris işlemleriyle tekrar yazmalısınız. Aşağıda birkaç örnek bulacaksınız.
1'den 7'ye kadar 2 atlayarak döngü oluşturalım ve i'yi ekrana basalım:
for i=1:2:7 i end
i = 1 i = 3 i = 5 i = 7
Verilen bir vektör üstünde döngü oluşturalım. İçine bir de if kontrolü koyalım.
for i=[5 13 -1]
if (i > 10)
disp([int2str(i) ' sayısı 10dan büyük'])
elseif i < 0
disp([int2str(i) ' sayısı negatif bir sayı'])
else
disp([int2str(i) ' sayısı 0 ile 10 arasında'])
end
end
5 sayısı 0 ile 10 arasında 13 sayısı 10dan büyük -1 sayısı negatif bir sayı
Başka bir örnek: A adında mxn'lik bir matris ve v adında 1xn'lik bir vektör verilmiş olsun, v'yi A'nın her satırından çıkarmak istiyoruz.
m = 6; n = 3; A = ones(m, n) v = 2 * rand(1, n)
A = 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 v = 1.6797 0.8537 1.2632
Döngü kullanarak şöyle yapabiliriz
for i=1:m A(i,:) = A(i,:) - v; end
Aynı işlemi yalnızca matris işlemleri kullanarak da yapabilirdik. Peki nasıl?
A = ones(m, n) - repmat(v, m, 1)
A = -0.6797 0.1463 -0.2632 -0.6797 0.1463 -0.2632 -0.6797 0.1463 -0.2632 -0.6797 0.1463 -0.2632 -0.6797 0.1463 -0.2632 -0.6797 0.1463 -0.2632
Bu hali (özellikle bu işleme çok kez ihtiyaciniz varsa) işinizi hızlandıracaktır!
İşlemlere harcanan zamanı ölçmek isterseniz tic ve toc komutlarını kullanabilirsiniz. Ayrıntılı bilgi için bu yazıya bakabilirsiniz.
Döngüler koşullu işlemler içerse dahi vektörleme yapabiliriz.
Ör: mxn'lik A matrisi verilsin, aynı boyutta tüm değerleri sıfır olan bir B matrisi oluşturalım. Daha sonra B'ye, A'nın sıfırdan büyük olan elemanlarını kopyalayalım.
Döngü kullanarak hesaplama:
B = zeros(m,n);
for i=1:m
for j=1:n
if A(i,j) > 0
B(i,j) = A(i,j);
end
end
end
B
B = 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0
Tüm bu işlemler hiç dongu kullanmadan yapılabilir! A'nın 0'dan büyük elemanlarının indislerini buluruz. B'ye, A'da bulunan indislerdeki elemanları kopyalarız:
B = zeros(m,n); ind = A > 0
ind = 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0 0 1 0
B(ind) = A(ind)
B = 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0 0 0.1463 0
Değişkenleri/Oturumu Kaydetmek
Bugün oturduk, çalıştık... Yorulduk, aynı değişkenlerle sonradan çalışalım dedik...
Alttaki kullanım tüm calışma alanı değişkenlerini dosyam.mat dosyasına kaydeder. Bulunduğunuz klasöre bir göz atın, dosya orada duruyor mu bakalım?
save dosyam
Sadece a ve b değişkenlerini kaydetmek isteseydik:
save dosyam a b
Peki bu iki değişkeni kaydetmek değil de silmek isteseydik:
clear a b
Tüm değişkenleri silelim:
clear
Kaydettiğimiz değişkenleri geri yükleyelim
load dosyam
m-dosyaları ile Betikler ve Fonksiyonlar Yazma:
MATLAB ile betik dosyası oluşturma
MATLAB betikleri ".m" uzantısı olan ve MATLAB kodları içeren dosyalardır. Dosya içindeki değişkenler global çalışırlar ve o anki MATLAB oturumunda ortamda bulunan aynı isimdeki değiskenleri değiştirir. betigim.m adındaki bir betiği betigim yazarak komut satırından çalıştırabilirsiniz.
Mesela alttaki kodu betigim.m olarak kaydedin.
a = 10; b = 2*a;
Şimdi de komut satırından şunları girelim
a = 2; b = 3; betigim(); a
a = 10
b
b = 20
Görüldüğü üzere tanımladığımız değişkenler betik içinde yeni değerlere atandı. Bu tehlikeli olabilir. Gelin fonksiyon yazmaya geçelim.
MATLAB ile fonksiyon yazma
Fonksiyonlar da m-dosyalarıdır. Farklı olarak bir fonksiyonun ilk satırı söyle olmalıdır:
function [sonuc1, sonuc2, ..., sonucm] = fonksiyonum(arg1, arg2,...,argn)
Fonksiyonun adı dosya adı ile aynı olmalıdır. Örnegin fonksiyonum fonksiyonu fonksiyonum.m dosyasına koyulmalıdır. Örnek
olarak fonksiyonum.m ve digerfonksiyonum.m dosyalarına bakiniz.
Fonksiyonlar lokal ortamda çalışırlar. Yani ana çalışma alanındaki aynı isimdeki bir değişkeni kaybetme riskiniz yoktur.
Fonksiyonun sonucunda sadece sonuç olarak dönen değişkenler, çağıran fonksiyonun çalışma alanında görülür.
Örnekleri yapmadan önce aşağıdaki fonksiyonları çalışma dizininize kaydedin.
fonksiyonum.m:
Tek girdi argumanı alan ve tek değer döndüren örnek fonksiyon
function y = fonksiyonum(x) a = [-2 -1 0 1]; y = a + x;
digerfonksiyonum.m:
2 girdi argumanı alan ve 2 değer döndüren örnek fonksiyon
function [y, z] = digerfonksiyonum(a, b) y = a + b; z = a - b;
a = [1 2 3 4]; b = fonksiyonum(2 * a) a
b = 0 3 6 9 a = 1 2 3 4
Görüldüğü üzere a değeri değişmedi. Şimdi de iki değişken döndüren örneğimizi çağıralım
[c, d] = digerfonksiyonum(a, b)
c = 1 5 9 13 d = 1 -1 -3 -5
Grafik Çizdirme
Belki MATLAB'in en güçlü yanı çizebildiği çeşitli güzel grafiklerdir. Önce temel çizim fonksiyonumuz plot ile başlayalım.
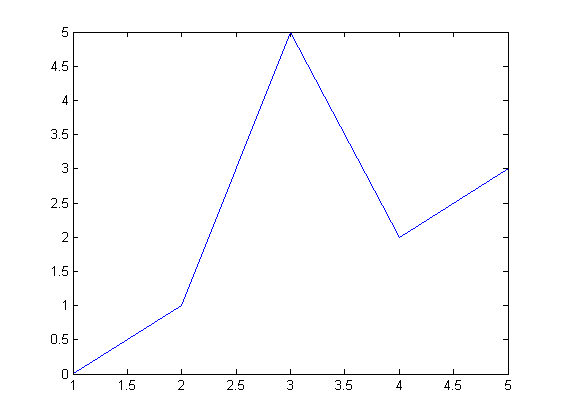
y = [0 1 5 2 3];
y'yi indis değerleri ile grafik olarak çizelim. Yani dikey eksen y'nin değerleri olsun, yatay eksense 1'den başlayıp y'nin boyuna kadar gitsin.
plot(y)
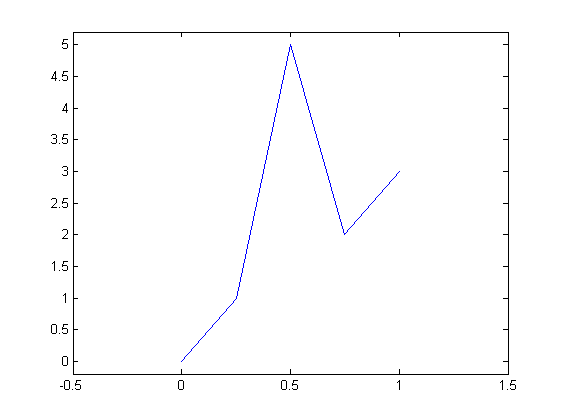
İstersek yatay eksen değerlerini de verebiliriz. Üstüne axis ile görüntülenen sınırları belirleyebiliriz. Kullanımı: axis([enkucukx enbuyukx enkucuky enbuyuky]):
x = linspace(0,1,length(y)); plot(x, y); axis([-0.5 1.5 -0.2 5.2]);
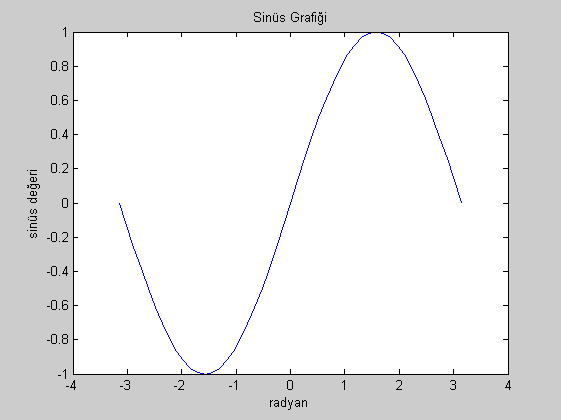
Normalde yeni bir figür çizdiğimizde en son aktif olan figürün üstüne çizilir. Eğer yeni bir figür açmak istersek figure yazabiliriz. Şimdi de bir sinüs grafiği çizelim ve biraz da süsleyelim.
figure
x = pi*[-24:24]/24;
plot(x, sin(x))
xlabel('radyan')
ylabel('sinüs değeri')
title('Sinüs Grafiği')
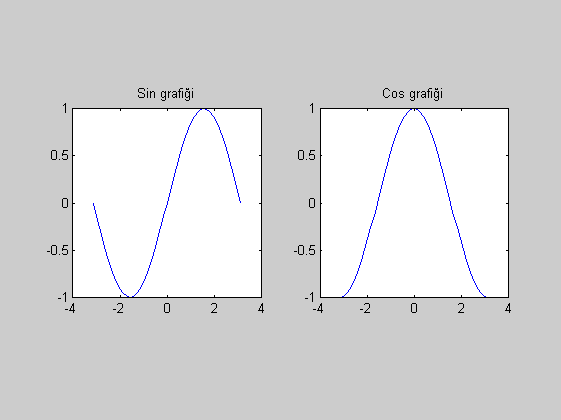
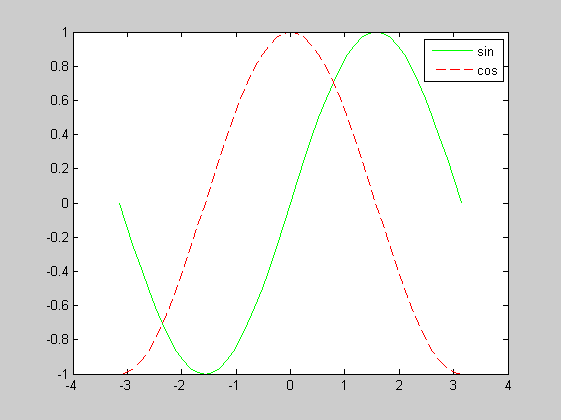
Bazen aynı figüre bir çizim yapmak yerine küçük pencereler halinde daha çok çizim yapmak isteyebiliriz. Bunun için de subplot imdadımıza yetişiyor. Kullanım: subplot(satır_sayisi, sütun_sayisi, su_an_cizilecek_olanin_indisi)
subplot(1, 2, 1)
plot(x, sin(x))
axis square
title('Sin grafiği')
subplot(1, 2, 2);
plot(x, cos(x));
axis square
title('Cos grafiği')
Yukarıda görüntülenen alanları kare yaptık. Başka seçenekler de koyabilirdik. F1'e basıp yardım belgelerinde arayarak veya komut satırına help axis yazarak ayrıntılı kullanımını görebilirsiniz.
Şimdi de aynı çizim alanına birden fazla çizim yapalım. Bunun için hold on ve hold off kullanmamız gerekecek. Bu komutlarla yeni çizim yapılırken eski çizimin üstüne yapılıp yapılmayacağı belirlenir. İstersek
plot(x1,y1,x2,y2,x3,y3,...) şeklinde de birden çok çizim yapabilirdik. Fakat böyle tercih etmemin sebebi çizimlerin özelliklerini ayrı ayrı belirleyebilmek.
Alttaki örnekte : parametresi kesik çizgili doğru çizer. help plot ile doğru ve nokta şekillerine bakabilirsiniz. Pek çok güzel seçenek mevcut. legend ile de çizimlerin adlarını koyabiliriz.
figure
plot(x, sin(x), '-g');
hold on
plot(x, cos(x), '--r')
legend('sin', 'cos')
hold off
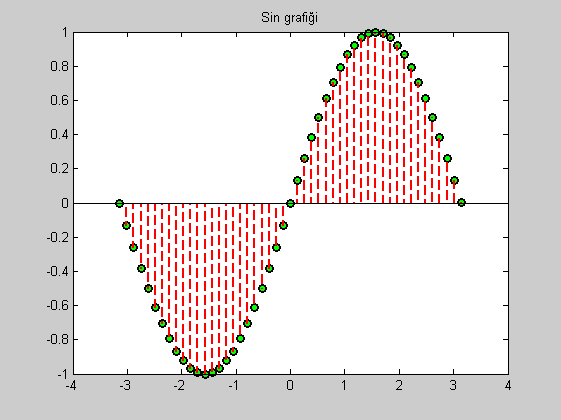
Bundan sonra tekrar çizim yapan fonksiyonlardan herhangi birini (plot, stem, bar, stairs, vb.) cağırırsanız eski çizim silinir ve sadece yeni çizim gözükür. Haydi örnek olarak stem fonksiyonunu çizelim, biraz da varyete ekleyelim.
stem(x,sin(x), '--ro','LineWidth',2,...
'MarkerEdgeColor','k',...
'MarkerFaceColor','g',...
'MarkerSize',7)
title('Sin grafiği')
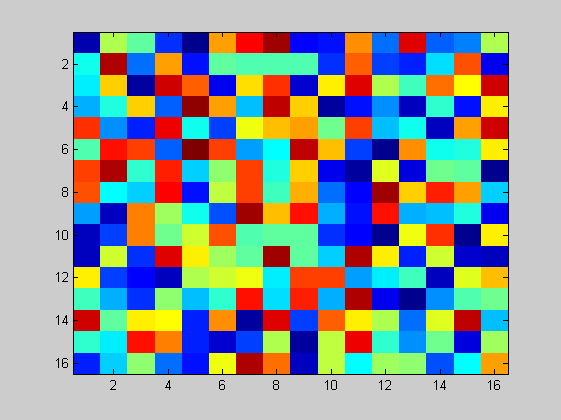
Matrisleri resim gibi çizmeye bakalım:
m = rand(16,16); imagesc(m)
Renklendirme haritasi olarak gri kullanalım, eksenleri silelim ve oranları pikseller kare görünecek şekilde sabitleyelim:
colormap gray axis image axis off
İşimiz bitti, tüm figürleri kapatalım. Not: Sadece close kullansaydık şu anki figürü kapatırdık.
close all
İpucu: Eğer döngülerin içinde plot fonksiyonunu (veya diğer çizim fonksiyonlarını) cağırırsanız her döngüdeki sonuç yerine son sonucu gorebilirsiniz. Tüm çizim sonuçlarını animasyon şeklinde görmek için plot fonksiyonundan sonra döngü içine drawnow komutunu giriniz.
Karmaşık Sayılarla İşlemler
MATLAB'de gerçel sayılar dışında karmaşık sayılarla da işlem yapılabilir. Karmaşık sayılar için "complex" veri tipi vardır. Karmaşık sayıları tanımlarken sanal değerleri için i veya j kullanılabilir. Daha önceden i veya j'yi başka değerlere atadıysanız (örneğin bir döngüde sayaç olarak) sanal birim olarak kullanamazsınız. Bu sebeple alternatif olarak 1i veya 1j seçeneklerini kullanmak daha iyi olacaktır. i'nin katları için de 4i, 7j gibi kullanabilirsiniz.
1i
i =
0 + 1.0000i
1j
j =
0 + 1.0000i
Değişik karmaşık sayılar oluşturalım
x = 1 + 4i
x = 1.0000 + 4.0000i
x = real(x) + imag(x)*1i
x = 25
theta = pi/4 y = cos(theta) + sin(theta)*1j
theta = 0.7854 y = 2.8284
Yukarıdaki örneği, Euler formülünü kullanarak da hesaplayalım, bakalım aynı mı?
y = exp(1i*theta)
y = 111.3178
Skalar değerler gibi, vektör ve matrisleri oluşturmak da mümkün:
v = [x y 5-7i]
v = 1.0e+002 * 0.2500 1.1132 0.0500 - 0.0700i
A = [v;4+1i 3-8j -2-2j]
A = 1.0e+002 * 0.2500 1.1132 0.0500 - 0.0700i 0.1000 0.0300 - 0.0800i -0.0200 - 0.0200i
B = rand(size(A)) + rand(size(A))*1i
B = 1.2382 5.5190 1.2364 4.4993 3.3112 2.2622
Şimdi transpoze ve eşlenik transpozeyi tekrardan hatırlayalım. Sadece tek tırnak koyarsak, bu elemanların eşleniğini de alır.
Eşlenik almadan transpoze yapmak istersek .' kullanmalıyız.
C1 = B'
C1 = 1.2382 4.4993 5.5190 3.3112 1.2364 2.2622
C2 = B.'
C2 = 1.2382 4.4993 5.5190 3.3112 1.2364 2.2622
Gerçel sayılardaki tüm işlemler karmaşık sayılarla da yapılabilir. Örneğin toplama, çıkarma, matris çarpımı, eleman eleman çarpım, fonksiyonlar, vb.
A + B
ans = 1.0e+002 * 0.2624 1.1684 0.0624 - 0.0700i 0.1450 0.0631 - 0.0800i 0.0026 - 0.0200i
B
ans = 1.0e+002 * 0.2376 1.0580 0.0376 - 0.0700i 0.0550-0.0031 - 0.0800i -0.0426 - 0.0200i
A * A'
ans = 1.0e+004 * 1.3091 0.0588 + 0.0915i 0.0588 - 0.0915i 0.0181
A .* B
ans = 1.0e+002 * 0.3095 6.1436 0.0618 - 0.0865i 0.4499 0.0993 - 0.2649i -0.0452 - 0.0452i
sum(sum(A(:,1) * B(2,:)))
ans = 352.5467
mean(B(:))
ans = 3.0110
Bazı fonksiyonlar karmaşık değerler döndürebilir. Örneğin hızlı Fourier dönüşümü karmaşık sayılar döndürür.
x = rand(8,1)
x = 0.7319 0.0405 0.4245 0.5402 0.9538 0.2089 0.1163 0.6462
y = fft(x)
y = 3.6624 -0.2661 - 0.1141i 1.1448 + 0.9370i -0.1778 + 0.5022i 0.7907 -0.1778 - 0.5022i 1.1448 - 0.9370i -0.2661 + 0.1141i
Sanırım başlangıç için bu kadar yeterli! Takıldığınız yerde MATLAB'in yardımını kullanabilirsiniz.
Artık rahatça resimleri matris şeklinde okuma ve üzerinde işlem yapma konularına geçebiliriz. Bir dahaki yazıda kaldığımız yerden devam edelim.



17 yorum
ismail bey size yeni bir tutorial konusu için öneri getirmek istiyorum. görüntü işleme işaret işlemenin bir alt dalı ve maalesef işaret işlemede genellikle okullarda olayın matematiksel yönünü olayın kendisiyle ilişkilendirmekten ziyade tamamen matematiksel yönünüyle alakalı bir eğitim veriliyor. işte tam bu noktada yeni konu olarak konvolusyon, fourier transformu, dft, dtft, fft…gibi işaret işlemenin içindeki geçen konuların matematiksel yönünden ziyade mantıksal yönüyle alakalı bir tutorial hazırlamanızın faydalı olacağına inanıyorum ve de neden mantıksal yönü üzerine vurgu yaptığımla alakalı bir örnek vermek istiyorum:
mesela iki boyutlu görüntü işleme iki uzaysal değişkene sahip fonksiyonun fouirer transformu alınınca ortaya çıkan dönüşüm fonksiyonunda frekans cinsinden w1, w2 değişkenleri bulunur falan filan diye giden bir matematiksel anlatım var ve olayın matematiksel yönüyle alakalı bir sorunum yok lakin neden bu ilahi dönüşüm yapılıyor, yani bu hastalığı iyileştiren mucizevi ilacın sırrı ne…
bu sadece bir örnekti…işaret işlemede bu gibi kavramların mantıksal yönüyle alakalı bir tutorialin çok işe yarayacağının tekrar üstüne basar çalışmalarınızda başarılar dilerim…
MATLAB’de bir değişkene atama yapılan herhangi bir satırın sonuna noktalı virgül koymazsan, o değişkenin yeni değerini ekrana basar. Alttaki iki satırı denersen farklarını görebilirsin:
resim1 = imread('resmim.jpg'); resim2 = imread('resmim.jpg')Tabii resim çok büyükse tümünü ekrana basmak yerine bir kısmını da basabilirsin, örneğin ilk 10luk kare bölgeyi görelim:
İsmail Bey, çok yararlı bir paylaşım yapmışsınız ellerize sağlık. Çok işime yaradı sizin sayenizde matlab öğrenmeye başladım
Matlab sınavıma çalışıyordum fakat bir sorum olacaktı. Bir program yazıyorum döngüde belli bir sayıdan sonra sonuç örneğin 123456e+018 biçiminde çıkıyor ben bunu tam sayı biçiminde istiyorum ya da rasyonel farketmez bunu m-file’da kodları yazarken nasıl kodlamam gerekiyor.
Öncelikle basamak sayısını bulan bir fonksiyon olsun:
basamakSayisi = @(x) length(sprintf('%d', x));Sonra herhangi bir tamsayıyı (tamsayı olduğundan emin olun), şöyle görüntüleyebilirsiniz:
ismail bey kofaktör dizeyi hakkında bilgi alabilirmiyim? araştırdım, help dosyasını insledim ama bulamadım. yardımcı olursanız çok sevinirim.
Kofaktör dizeyinden kastınız “Matrix of cofactors” olmalı.
İlgili sayfadaki arabölüme ve hemen altındaki “Adjugate” arabölümüne bakarsanız oradaki formülden kofaktör matrisinin şu şekilde hesaplanabileceğini çıkarabilirsiniz:
Herhangi bir A dizeyinin koföktörü, bu dizeyin determinantı ile tersinin devriğinin çarpımıdır. Yani kısaca
Matlabda global değişkenler nasıl kullanılır ?
Mesela bir fonksiyonunmuz var
[P,m]=gonder(str,m)
ana programdan olsun. Burada P
P(i).ad=str olsun fonksiyon içinde
fonksiyondan ana programa donerken P(i).ad= ” boşluk olarak donuyor acaba sorun ne?
Sayafnız cok yararlı ve cok ilgilimi cekti. Bunun için tesekkurler… Paylaşımlarınızda cok yararlı … Eğer cevaplarsanız cok sevineceğim bir sorum var … Matlabda struct arrayler ile ilgili …
Aşağıdaki örnek yapımız :
Yapi(i).ad =’Mehmet’
Yapi(i).sad =’Ak’
Yapi(i).oran =3.45
şeklinde oluştuğunu düşünürsek,
fprintf(‘%s %d’,yapi(i).ad,yapi(i).oran)
ile ekrana bu bilgileri yazdığımızda karşımıza :
Mehmet 3.450000 >> geliyor. Normal bir şekilde bunu nasıl yazdırabiliriz ? (; eklemeklemi ?)
Bunun yanında
Bu yapi değişkenini fprintf ile bazen yazdırabiliyorum ama bir fonksiyon içinde kullandığım zaman kesinlikle hata mesajı alıyorum buradaki parantezlerden dolayı olduğunu sanıyordum bunun için{ } parantezlerini kullandım bazen oldu ama çoğu zaman olmuyor. (Buda çok garibime gitmişti …)
Hata mesajıda :
??? Error using ==> fprintf
Function is not defined for ‘cell’ inputs.
Error in ==> Listele at 27
fprintf(‘Kalan %d . kaydin adi : %s orani ise %3.5f\n’,i,yapi(i).ad,yapi(i).oran)
Error in ==> sistem_a at 151
Listele(s)
Not : Böyle bir struct yapı içindeki dizinin herhangi bir elemanının ad veya oran adlı değerlerini birlikte nasıl yazırabiliriz? Sorun acaba biri float diğeri string diyemi ? ve neden normal program içinde yazıyorda fonksiyona gecince bu hatayı veriyor. İlgilenirseniz çok sevinirim …
Mail adresim : [email protected]
Yararlı bir yazı. Çok teşekkürler.
yazı için çoook ama çok teşekkürler…
görüntü işleme ile uğraşmak istiyorum.programlama bilgim giriş seviyesinde.sizce matlab ile mi yoksa opencv ile mi başlamalıyım.
Teşekküler. Bu yapacağınız işe bağlı. Bence konu ile ilgili OpenCV’de halihazırda yazılmış fonksiyonlar var mı diye bakabilirsiniz. Eğer varsa ve işleri “gerçek zamanlı” yapmak gibi bir hedefiniz varsa OpenCV kullanmanızı öneririm. Ama gerçek zamanlı olması hedefiniz yoksa MATLAB kullanabilirsiniz. Resim ve görüntü işlemede MATLAB da çok hünerlidir. Belki aradığınız şeyi yapan bir kaynak MATLAB file exchange’de vardır.
MATLAB de sadece toplama işlemi kullanılarak sinx değeri nasıl hesaplanır?
Yapamazsınız. Çarpma da lazım. Sinüs’ün Taylor serisi şeklinde yazımına bakın.
x=0:0.001:2*pi
sin(x), cos(x), ve exp(x) fonksiyonları her x değeri için aşağıda terim (eleman) sayısı belirtilen seri açılımları kullanılarak hesaplanacak.
önce seri açılımında 1 elamanı ile daha sonra 3 eleman kullanılarak,
en sonda ise 10 eleman kullanılarak ayrı ayrı grafikleri çizilecek
bunu nasıl yapabilirim yardımcı olabilir misiniz?
x=0:0.001:2*pi
sin(x), cos(x), ve exp(x) fonksiyonları her x değeri için aşağıda terim (eleman) sayısı belirtilen seri açılımları kullanılarak hesaplanacak.
önce seri açılımında 1 elamanı ile daha sonra 3 eleman kullanılarak,
en sonda ise 10 eleman kullanılarak ayrı ayrı grafikleri çizilecek
bunu nasıl yapabilirim yardımcı olabilir misiniz?
Matlab da konvolüsyon konusunu araştırırken sitenizi gördüm de acaba bu konuda bilgi verebilir misiniz diziler üzerinde konvolüsyon yontemini yapmam ve bunu grafik olarak da göstermem gerekiyor nasıl yapabilirim acaba? özellikle grafik kısmı için yardımcı olursanız sevinirim…. Kolay gelsin…